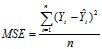Pada tahap ini dari beberapa model ARIMA yang mungkin dipilih hanya satu model yang terbaik, setelah terpilih model yang terbaik maka di bentuk model ARIMA-nya.
1. Pemilihan Model Terbaik
Untuk menentukan model yang terbaik dapat digunakan standard error estimate berikut:
Dimana:
Yt : nilai sebenarnya pada waktu ke-t
Model terbaik adalah model yang memiliki nilai standard error estimate (S) yang paling kecil. Selain nilai standard error estimate, nilai rata-rata kuadrat kesalahan peramalan
(MSE) dapat juga digunakan sebagai bahan pertimbangan dalam menentukan model yang terbaik yaitu:
Dimana:
n : Jumlah data
2. Peramalan
Notasi yang digunakan dalam ARIMA adalah notasi yang mudah dan umum. Misalkan model ARIMA (0,1,1)(0,1,1)12 dijabarkan sebagai berikut:
(1-B)(1-B12)Zt = (1-ϕ1B)( 1- ϕ 1B12)et
Tetapi untuk menggunakannya dalam peramalan mengharuskan dilakukan suatu penjabaran dari persamaan tersebut dan menjadikannya sebuah persamaan regresi yang lebih umum. untuk model diatas bentuknya adalah:
Untuk meramalkan satu periode ke depan, yaitu Xt+1 maka seperti pada persamaan berikut:
Nilai et+1 tidak akan diketahui, karena nilai yang diharapkan untuk kesalahan random pada masa yang akan datang harus ditetapkan sama dengan nol. Akan tetapi dari model yang disesuaikan (fitted model) boleh diganti nilai et, et-11 dan et-12 dengan nilai yang ditetapkan secara empiris (seperti yang diperoleh setelah iterasi terakhir algoritma Marquardt). Tentu saja jika meramalkan jauh ke depan, tidak akan kita peroleh nilai empiris untuk “e” sesudah beberapa waktu, dan oleh sebab itu nilai harapan nilai-nilai tersebut akan seluruhnya nol. Untuk nilai Z, pada awal proses peramalan, akan diketahui nilai Zt, Zt-11, Zt-12. Akan tetapi sesudah beberapa saat, nilai Z akan berupa nilai ramalan (forecasted value), bukan nilai-nilai masa lalu yang telah diketahui.